Proof :
Lemma 1b is the obvious counterpart of lemma 1a, and will be proved using the
same arguments. If b is the closest point of B from a, then a
circle C of radius ab centered at a contains only one point of B,
namely b. The tangent to C is thus a supporting line of B.
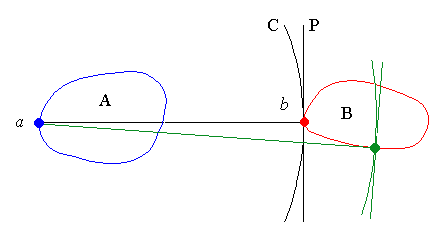
Similarly to the second part of lemma 1a, if some points of B are on the same side of P than A, then the support point is not the closest point of B from a. This is opposed to the definition Hausdorff distance.