An O(n) Time Algorithm for Finding an Ear
A recursive algorithm was developed by Hossam ElGindy at the University of Newcastle, Hazel Everett at the Université du Québec, and Godfried T. Toussaint at McGill University [1].
The input is a good sub-polygon GSP and a vertex pi. Initially, the function FindAnEar is called with the simple polygon P and any vertex of P.
Function FindAnEar(GSP, pi)
1. if pi is an ear then
2. return pi
3. Find a vertex pj such that
(pi, pj) is a diagonal of
GSP.
Let GSP' be the good sub-polygon of GSP
formed by
(pi, pj).
Re-label the vertices of
GSP' so that pi = p0 and
pj = pk-1
(or pj =
p0 and pi = pk-1
as appropriate) where k is the number
of vertices of GSP'.
4. FindAnEar(GSP', floor(k/2))
End FindAnEar
The correctness of the algorithm follows from Lemmas 1, 2, and 3.
Lemma 1: A good sub-polygon has at least one proper ear.
Proof: Let (pi, pj) be the
cutting edge of GSP. By the
Two-Ears Theorem GSP has at
least two non-overlapping ears. Vertices pi and
pj cannot be the only ears of GSP since these
would overlap. Thus some other vertex of GSP is an ear and it is
a proper ear.
Q.E.D.
Lemma 2: A diagonal of a good sub-polygon GSP splits GSP into one good sub-polygon and one sub-polygon that is not good.
Proof: GSP contains exactly one edge, the cutting edge, which is not an edge of P. The cutting edge is entirely contained in one of the sub-polygons formed by the diagonal. Then the other sub-polygon is a good sub-polygon since it consists of edges of P and the diagonal which becomes its cutting edge.
Q.E.D.
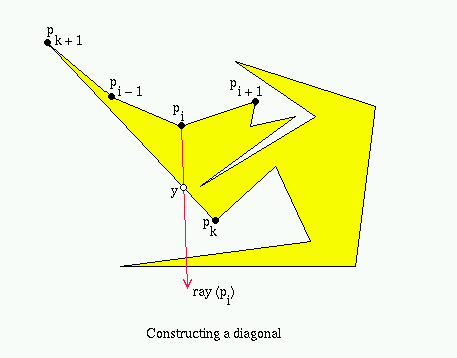
Lemma 3: If vertex pi is not an ear then there exists a vertex pj such that (pi, pj) is a diagonal of P.
Proof: Given a vertex pi which is not an ear we
will show how to find a vertex pj such that
(pi, pj) is a diagonal. Construct a
ray, ray(pi), at pi that
bisects the interior of angle (pi-1,
pi, pi+1). Find the first
intersection point of ray(pi) with the boundary
of P. Note that this is done simply by testing each edge of the
polygon for intersection with ray(pi). Let
y be the intersection point on edge (pk,
pk+1). Point y must exist and y <>
pi-1 or pi+1. Note that the
line segment (pi, y) lies entirely inside P.
Thus if y is a vertex then (pi, y) is a
diagonal. Suppose y is not a vertex. Then pk+1
and pi-1 lie in one of the half-planes defined by
ray(pi), and pk and
pi+1 lie in the other. We will show that if triangle
(pi, y, pk+1) does not
contain a vertex pj such that (pi,
pj) is a diagonal of P then triangle
(pi, y, pk) does.
Q.E.D.
Q.E.D.
Line 1 of FindAnEar can be done in O(n) time where n
is the number of vertices in GSP. Line 2 takes constant time.
Line 3 can be done in O(n) time as well.
On the first two calls to FindAnEar, GSP has O(n)
vertices. Consider any subsequent call. Let k be the number of
vertices in GSP. We have i = floor(k/2) and
(p0, pk-1) the cutting edge of
GSP. Consider line 3. If 0 <= j <= i-2 then
GSP' = (pj, pj+1, ...,
pi). Otherwise, i+2 <= j <= k-1
and GSP' = (pi, pi+1, ...,
pj). In either case, GSP' contains no more
than floor(k/2) + 1 vertices.
This page was last updated on Wednesday, December 10th, 1997.
© 1997 Ian Inc.