 |
 |
 |
 |
| Molecules | Fonts | Motion Planning | Music |
 |
 |
 |
 |
| Manufacturing | Probability | Polyhedral Computation | Graph Drawing |
 |
 |
 |
 |
| Molecules | Fonts | Motion Planning | Music |
 |
 |
 |
 |
| Manufacturing | Probability | Polyhedral Computation | Graph Drawing |
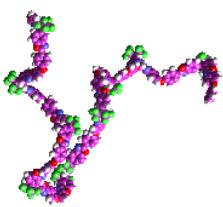 |
Molecular ReconfigurationIn chemistry and physics large molecules are often modelled as
polygonal linkages. Properties of these molecules can be
determined by geometric properties of the underlying linkages. The
purpose of this research is to study the combinatorial and algorithmic
aspects of polygonal linkages to help further our
understanding of how molecules reconfigure themselves. |
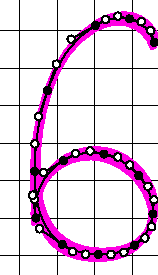
Font DesignIn font design, we study the
geometric, mathematical and methodological problems associated with
the simulation of handwriting, random typefaces, brushed characters,
running ink and linked letters. The character "6" on this
page is from a typeface designed from a sample written on a magnetic
pad. Our software identifies the important points of a stroke, creates
smooth Bézier curves, defines glyphs based on various pen nibs,
and outputs a Postscript font. |
 |
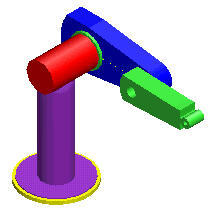 |
Robot Motion Planning
Robotic arms are frequently used in manufacturing plants to perform
tasks such as welding, screwing and drilling. Geometric questions
in robotic motion planning involve finding efficient
motion plans for a given robotic arm and determining what kinds
of tasks a given robotic arm can and can not do.
|
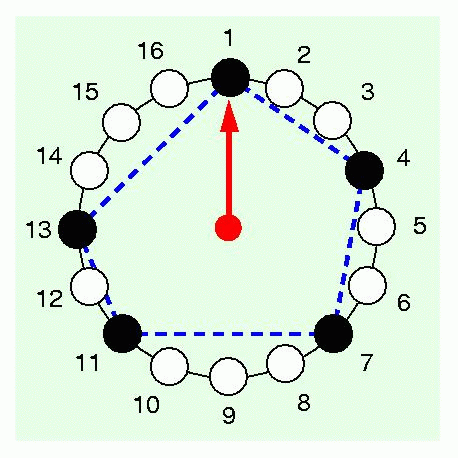
Computational Geometric Problems in MusicSymbolic music, particularly rhythm and melody, are studied from the geometric and algorithmic points of view. In particular, we are interested in(1) methods for visualizing, representing, and comparing the similarity of rhythms and melodies, (2) developing mathematical measures of syncopation, (3) applying music theory to ethnomusicology, (4) applying pattern recognition tools to music information retrieval, and (5) applying tools from bioinformatics, such as phylogenetic analysis, to aid in the determination of a phylogeny of world rhythms. |
 |
 |
Geometric Problems in ManufacturingThere are many
interesting geometric problems that arise in manufacturing. A typical
example of the problems we study is the problem of finding a stable
grip on an object with a robotic hand consisting of two parallel
rectangular plates. The diagram on the left illustrates a particularly
challenging case. |
Probabilistic AnalysisWe study the expected behavior of algorithms and data
structures
under random input or artificial randomization. Our work builds on
elementary probability theory rather than combinatorial
analysis. Subtopics of particular interest include random number
generation and random trees. For example, we create models of random
trees for simulating virtual forests. The tree on this page is a
binary search tree built from a Weyl sequence (e), (2e), (3e),
etcetera, where (.) denotes modulo 1. |
 |
 |
Polyhedral ComputationThe theory of convex polytopes has its origins in the study of systems of linear inequalities. A (convex) polyhedron is the set of solutions to a system of linear inequalities. A bounded polyhedron is called a polytope. The vertices of a polytope are those feasible points that do not lie in the interior of a line segment between two other feasible points. Converting from the halfspaces to the vertices is called vertex enumeration. An important open problem is the existence of a vertex enumeration algorithm polynomial in the number of halfspaces plus the number of vertices. We distribute the lrs library which performs a number of related functions, including vertex/facet enumeration, redundancy removal, computing Nash equilibria and Fourier elimination. We are also interested in applications of polyhedral computation to a wide number of areas, most recently to quantum information.David Avis |
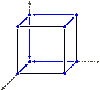
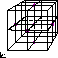
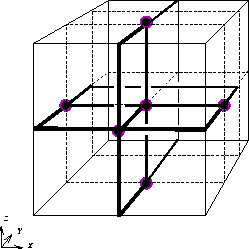
Graph DrawingWe study the layout of graphs and diagrams. For example, the
picture
here illustrates a 3-dimensional orthogonal grid layout of a graph.
|
 |
|
|
|
|
|
|
|
|
|